LOGARITMACIÓN

RADICACION Y LOGARITMACION DE 

LOS NUMEROS REALES

1. 1. RADICACION DE NUMEROS REALES OBJETIVOS. Distinguir la radicación como característica de los exponentes fraccionarios. Utilizar los radicales para afianzar la similitud con la potenciación como operación inversa de ésta. Resolver operaciones con exponentes fraccionarios, empleando las propiedades como herramienta de la simplificación INSTITUCION EDUCATIVA LA INMACULADA. TIERRALTA - CORDOBA AREA DE MATEMÁTICAS. LIC. OMAR MORA
2. 2. CONCEPTO DE RAIZ En estricto rigor, raíz es una cantidad que se multiplica por sí misma una o más veces para presentarse como un número determinado. Para encontrar esa cantidad que se multiplica se recurre a la operación de extraer la raíz a partir del número determinado y se ejecuta utilizando el símbolo √, que se llama radical. Por ello es que se habla de operaciones con radicales al referirse a operaciones para trabajar con raíces. Encontrar o extraer la raíz es realizar la operación contraria o inversa de la potenciación, así como la suma es la operación inversa de la resta y viceversa, y la multiplicación es la operación contraria de la división y viceversa. Los nombres de las partes que constituyen cada operación matemática son: X: Base de la potencia X: Valor de la raíz n: Exponente de la potencia n: Índice de raíz a: Valor de la potencia a: Cantidad subradical (o radicando)
3. 3. PROPIEDADES DE LA RADICACION Debido a que las raíces pueden convertirse a potencias de exponente fraccionario, cumplen con todas las propiedades de potencias a partir de las cuales se pueden deducir las siguientes propiedades de raíces: Multiplicación de raíces de igual índice: Se multiplican las bases y se conserva el índice. 1. Multiplicación de raíces de igual índice Según una propiedad de los radicales: Esto significa que si dos números están multiplicándose dentro de una raíz, se puede extraer la raíz de cada uno de ellos en forma separada y luego multiplicarlos; o también que si hay dos raíces de igual grado multiplicándose se pueden multiplicar los números y obtener la raíz después. Ejemplo 1: Dentro de la raíz cuadrada tenemos una multiplicación (9x4), sacamos la raíz cuadrada a cada uno de los números para finalmente multiplicarlos.
4. 4. EJEMPLO .
5. 5. 2. DIVISIÓN DE RAÍCES DE IGUAL ÍNDICE: Se dividen las bases y se conserva el índice. EJEMPLO 1.
6. 6. 3. RAÍZ DE RAÍZ: Para obtener raíz de raíz se multiplican los índices y se conserva la base. EJEMPL O
7. 7. 4. RAÍZ DE UNA POTENCIA CUYO EXPONENTE ES IGUAL AL ÍNDICE: 5. PROPIEDAD DE AMPLIFICACIÓN. Tanto el índice como el exponente de la potencia pueden amplificarse por un mismo valor.
8. 8. 6. INGRESO DE UN FACTOR DENTRO DE UNA RAÍZ: Para introducir un factor dentro de una raíz se coloca el factor dentro del radical como potencia con exponente igual al índice y multiplicando a los demás factores. Observación: las propiedades anteriores son válidas solamente en el caso de que las raíces estén definidas en los números reales. EJEMPLO
9. 9. 7. POTENCIA DE RADICALES. EJEMPLOS.

10. LOGARITMACIÓN

    Los logaritmos fueron ideados antes de las computadoras actuales que permiten realizar operaciones con números muy grandes o muy pequeños. El logaritmo simplifica el cálculo siempre y cuando no contemos con una calculadora científica. A medida que se analizaron más y más los logaritmos se fueron ideando muchas propiedades que simplifican aun más el cálculo. Es verdad que muchos de dichos cálculos se pueden hacer actualmente con la ayuda de las computadoras. Pero en algunas ocasiones se encontrarán explicaciones de ciertos temas utilizando logaritmos y no podremos entenderlas a menos que tengamos una base sólida en el tema. 
    
    

      La Logaritmación es una operación entre dos números reales a y b, llamados base y argumento respectivamente, que se define como sigue: (lo hacemos mediante ejemplo para que puedas entenderlo)
    log ₂ 8 =      3                pues 2³ = 8  
    log ₄ 16 =     2                pues 4² = 16 
    log ₆ 1 =       0                pues 6⁰ = 1 
    log ₁₆ ¼ = -1/2               pues 16^-1/2 = 1/4

Potenciación de números reales

Potenciación de números reales

Todo producto de factores iguales, por ejemplo: a·a·a puede escribirse abreviadamente así: a³.

En la expresión anterior, a³ se llama potencia, el factor que se repite (a) se llama base y el numero de veces que se repite el factor (3) se llama exponente.

Potencias con exponente entero

Con exponente racional o fraccionario

 

 

adicion y sustraccion de numeros reales

Adicion De Numeros Reales"

1. 1. Adición de Números Reales Propiedades Matemática 9no Grado Haz Clic sobre la mano para Entrar Créditos
2. 2. La Adición de Números Reales Para sumar dos o más números reales , Suma de tres cifras decimales a) 2,04721 + 5,9826 + 0,2537 = Mejor aproximación: 2,047 + 5,983 + 0,254 debemos escribir la mejor aproximación de cada uno de los sumando con n cifras decimales y luego efectuamos la suma el resultado será la suma aproximada de los números reales con sus cifras decimales . Resultado 2,047 + 5,983 + 0,254 = 8,284 Siguiente Atrás
3. 3. Propiedades de la adición C o n m u t a t i v a Si a € R y b € R entonces Si un numero “a” pertenece al conjunto de numero reales R, y un numero “b” pertenece al conjunto de números reales R entonces: a + b = b + a Siguiente Atrás
4. 4. Propiedades de la adición C o n m u t a t i v a Ejemplo 2,045 + 1,87 = 3,915 El orden de los sumando no altera la suma 1,87 + 2,045 = 3,915 Siguiente Atrás
5. 5. Propiedades de la adición A s o c i a t i v a Si a € R, b € R y c € R entonces Si un numero “a” pertenece al conjunto de numero reales R, el numero “b” pertenece al conjunto de números reales R y el número “c” pertenece al conjunto de numeros reles R entonces: (a + b) + c = a + (b + c) Siguiente Atrás
6. 6. Primero sumamos los números que están entre paréntesis Propiedades de la adición Ejemplo: Sean los números 4,724, 0,87 y 2,6543; efectuemos la suma con tres cifras decimales (4,724 + 0,87) + 2,6543 = (5,631) + 2,6543 = 9,285 A s o c i a t i v a (5,631) + 2,6543 = Luego le sumamos el resultado al tercer numero Siguiente Atrás
7. 7. Propiedades de la adición E l e m e n t o n e u t r o Si a € R, entonces Si un numero “a” pertenece al conjunto de numero reales R, entonces: a + 0 = 0 + a = a Al sumar cualquier número real con 0, se obtiene el mismo numero real. Siguiente Atrás
8. 8. Propiedades de la adición Ejemplo: 1,759 + 0 = 1,759 E l e m e n t o n e u t r o 0 + 1,759 = 1,759 Siguiente Atrás
9. 9. Propiedades de la adición E l e m e n t o S i m e t r i c o O p u e s t o Si a € R, existe un único (-a) tal que a + (-a) = 0 Si un numero “a” pertenece al conjunto de numero reales R, entonces: a + (-a) = 0 Al sumar cualquier número real, con su simétrico u opuesto, se obtiene como resultado 0. Siguiente AtrásLa resta es la operación inversa de la suma, es una operación entre dos números: el minuendo y el sustraendo. Siempre que se tengan dos números reales, se pueden restar; por ejemplo:

   13,2 – 17,8 = –4,6

   Minuendo – sustraendo = resto
   Al efectuar restas hay que tener cuidado con los signos de los números.
   Al efectuar sustracciones o restas deben considerarse las siguientes reglas de los signos:
   • Si el minuendo y el sustraendo son positivos, y el minuendo es mayor que el sustraendo, se efectúa la resta y el resultado es positivo.
   Por ejemplo:

   27,8 – 12,1 = 15,7

   • Si el minuendo y el sustraendo son positivos, y el minuendo es menor que el sustraendo, se efectúa la resta y el resultado es negativo.
   Por ejemplo:

   12,1 – 27,8 = –15,7

   • Si el minuendo es negativo y el sustraendo es positivo, se efectúa la suma de ambos números y al resultado se le pone el signo menos.
   Por ejemplo:

   –21,8 – 12,1 = –33,9

   • Restar un número positivo es lo mismo que sumar un número negativo.
   Por ejemplo:

   27,8 – 12,1 = 27,8 + (–12,1) = 15,7

   • Restar un número negativo es lo mismo que sumar un número positivo.
   Por ejemplo:

   27,8 – (–12,1) = 27,8 + 12,1 = 33,9 –27,8 – (–12,1) = –27,8 + 12,1 = 12,1 – 27,8 = –15,7

   Aunque la resta está muy emparentada con la suma, no tiene todas las propiedades de la suma.
   Por ejemplo, la resta no es una operación conmutativa:

   54,2 – 33,1 = 21,1

   y ese resultado es distinto de

   33,1 – 54,2 = –21,1

10. 
    

 multiplicación de números reales 

La multiplicación es una suma abreviada. Por ejemplo, si necesitamos escribir 8 + 8 + 8 + 8 + 8 + 8, esto es, sumar 6 ochos, para no escribir tanto, el mundo se puso de acuerdo y mejor lo escribimos como 6 x 8. De la misma manera 7 x 5 quiere decir sumar 7 cincos (o también sumar 5 sietes. ¿Podrías decir por qué es lo mismo sumar 5 sietes que sumar 7 cincos?). También como resultado de esto nos tuvimos que aprender las tablas de multiplicar para hacer operaciones rápidamente. Las tablas de multiplicar de la aritmética siguen siendo válidas aquí.

Los números que se multiplican se llaman factores y el resultado se llama el producto o multiplicación

La multiplicación con números reales tiene una dificultad adicional. Como tenemos que multiplicar tanto números positivos como negativos, nos tenemos que aprender la tablita siguiente:

División de números reales 

De la misma manera que para definir la resta recurrimos a algo que ya sabíamos, como era la suma, para definir la división de números reales recurrimos a cosas ya conocidas, en este caso la multiplicación.

Tenemos el siguiente problema ¿Por cuánto debo multiplicar a un número a para obtener otro número b?. Esto es . Recordemos lo que hicimos para la resta. En este caso solo sabemos multiplicar así que llamamos a la interrogación x, y multiplicamos ambos miembros de esta igualdad por el inverso multiplicativo de a, tenemos:

 De aquí tenemos: 

y por lo tanto el número desconocido x es:

Pero es mejor utilizar el símbolo b ÷ a , que lo leeremos como b entre a, en lugar de la letra x. Por lo tanto tenemos qué:

Nota: Si sustituimos este número encontrado

en el lugar de la interrogación de la pregunta inicial, podemos comprobar que realmente resuelve el problema inicial que planteamos: “¿Por cuánto debo multiplicar a un número a para obtener otro número b?” porque: 

Diremos que dividir un número b (llamado dividendo) entre otro número a (llamado divisor) es multiplicar al número b, por el inverso multiplicativo del número a. En otras palabras, para realizar una división debemos convertirla primero en una multiplicación utilizando el inverso multiplicativo del divisor. Para indicar una división utilizamos el signo entre (÷).  Así por ejemplo p ÷ q  quiere decir dividir p entre q;  -45÷10  significa dividir -45 entre 10.

Lo anterior quiere decir que si tenemos que dividir dos números, debemos convertir la división en una multiplicación del dividendo por el inverso multiplicativo del divisor.

Ejemplo: ; 

Notación científica

La notación científica, y también denominada patrón o notación en forma exponencial, una forma es escribir los números que acomoda valores demasiado grandes (100000000000) o pequeños (0,00000000001)¹ para ser convenientemente escrito de manera convencional.^2 3 El uso de esta notación se basa en potencias de 10⁴ (los casos ejemplificados anteriormente en notación científica, quedarían 1 × 10¹¹ y 1 × 10⁻¹¹, respectivamente). Como ejemplo, en la Química, al referirse a la cantidad de entidades elementales (átomos, moléculas, iones, etc.), hay una cantidad llamada cantidad de materia (mol).⁵

Un número escrito en notación científica sigue el siguiente patrón:

El número m se denomina mantisa y e el orden de magnitud.⁶ La mantisa, en módulo, debe ser mayor que o igual a 1 y menor que 10, y la orden de magnitud, dada como exponente, es el número que más varía conforme al valor absoluto.

Operaciones matemáticas con notación científica[editar]

Adición y sustracción[editar]

El cerebro humano tiene cerca de 1 × 10¹¹ neuronas.³⁵

Para sumar o restar dos números en notación científica, es necesario que los exponentes sean los mismos. Es decir, uno de los valores debe ser transformado para que su exponente sea igual al del otro. La transformación sigue el mismo principio de equilibrio. El resultado probablemente no estará en forma estándar, siendo convertido posteriormente.³⁶

Ejemplos:

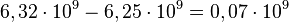 (no estándar) o  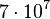(estandarizado)

Multiplicación[editar]

Multiplicar las mantisas y sumar los exponentes de cada valor. Probablemente, el resultado no será estándar, pero se puede convertir.³⁶

Ejemplo:

 (não padronizado)  (convertido a notación estándar)

(ya estandarizado sin necesidad de conversión)

División[editar]

Dividir las mantisas y restar los exponentes de cada valor. Probablemente, el resultado no será estándar, pero se puede convertir:³⁶

Ejemplos:

(estandarizado)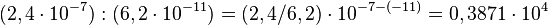

(no estándar) 

Exponenciación o Potenciación[editar]

La mantisa es elevada al exponente externo y el congruente de base diez se multiplica por el exponente externo.³⁶

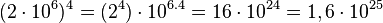(estandarizado)

Radicación[editar]

Antes de realizar la radicación es necesario transformar un exponente a un múltiplo del índice. Después de que se hace esto, el resultado es la radicación de la mantisa multiplicada por diez elevado a la relación entre el exponente y el índice de radical.³⁶