Notación científica

La notación científica, y también denominada patrón o notación en forma exponencial, una forma es escribir los números que acomoda valores demasiado grandes (100000000000) o pequeños (0,00000000001)¹ para ser convenientemente escrito de manera convencional.² ³ El uso de esta notación se basa en potencias de 10⁴ (los casos ejemplificados anteriormente en notación científica, quedarían 1 × 10¹¹ y 1 × 10⁻¹¹, respectivamente). Como ejemplo, en la Química, al referirse a la cantidad de entidades elementales (átomos, moléculas, iones, etc.), hay una cantidad llamada cantidad de materia (mol).⁵

Un número escrito en notación científica sigue el siguiente patrón:

m\ \times\ 10^{e}

El número m se denomina mantisa y e el orden de magnitud.⁶ La mantisa, en módulo, debe ser mayor que o igual a 1 y menor que 10, y la orden de magnitud, dada como exponente, es el número que más varía conforme al valor absoluto.

Operaciones matemáticas con notación científica[editar]

Adición y sustracción[editar]

El cerebro humano tiene cerca de 1 × 10¹¹ neuronas.³⁵

Para sumar o restar dos números en notación científica, es necesario que los exponentes sean los mismos. Es decir, uno de los valores debe ser transformado para que su exponente sea igual al del otro. La transformación sigue el mismo principio de equilibrio. El resultado probablemente no estará en forma estándar, siendo convertido posteriormente.³⁶

Ejemplos:

{4,2\cdot 10^{7}} + {3,5\cdot 10^{5}} = {4,2\cdot 10^{7}} + {0,035\cdot 10^{7}} = {4,235\cdot 10^{7}}

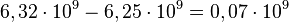{6,32\cdot 10^{9}} - {6,25\cdot 10^{9}} = {0,07\cdot 10^{9}}

(no estándar) o

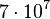{7\cdot 10^{7}}

(estandarizado)

Multiplicación[editar]

Multiplicar las mantisas y sumar los exponentes de cada valor. Probablemente, el resultado no será estándar, pero se puede convertir.³⁶

Ejemplo:

{(6,5\cdot 10^{8})}\cdot {(3,2\cdot 10^{5})} = {(6,5\cdot 3,2)\cdot 10^{8+5}} = {20,8\cdot 10^{13}}

(não padronizado)

{2,08\cdot 10^{14}}

(convertido a notación estándar)

{(4\cdot 10^{6})}\cdot {(1,6\cdot 10^{-15})} = {(4\cdot 1,6\cdot 10^{6+(-15)})} = {6,4\cdot 10^{-9}}

(ya estandarizado sin necesidad de conversión)

División[editar]

Dividir las mantisas y restar los exponentes de cada valor. Probablemente, el resultado no será estándar, pero se puede convertir:³⁶

Ejemplos:

{(8\cdot 10^{17})} : {(2\cdot 10^{9})} = {(8/2)\cdot 10^{17-9}} = {4\cdot 10^{8}}

(estandarizado)

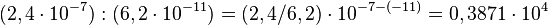{(2,4\cdot 10^{-7})} : {(6,2\cdot 10^{-11})} = {(2,4 / 6,2)\cdot 10^{-7-(-11)}} = {0,3871}\cdot 10^{4}

(no estándar)

{3,871}\cdot 10^{3}

Exponenciación o Potenciación[editar]

La mantisa es elevada al exponente externo y el congruente de base diez se multiplica por el exponente externo.³⁶

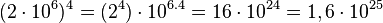{(2\cdot 10^{6})^4} = {(2^4)\cdot 10^{6.4}} = {16}\cdot 10^{24} = 1,6\cdot 10^{25}

(estandarizado)

Radicación[editar]

Antes de realizar la radicación es necesario transformar un exponente a un múltiplo del índice. Después de que se hace esto, el resultado es la radicación de la mantisa multiplicada por diez elevado a la relación entre el exponente y el índice de radical.³⁶

\sqrt{1,6\cdot 10^{27}} = \sqrt{16\cdot 10^{26}} = \sqrt{16}\cdot 10^{26/2} = 4\cdot 10^{13}

\sqrt[5]{6,7\cdot 10^{17}} = \sqrt[5]{670\cdot 10^{15}} = \sqrt[5]{670}\cdot 10^{15/5} \approx 3,674\cdot 10^{3}

Matematicas de octavo

martes, 18 de agosto de 2015

Notación científica

Operaciones matemáticas con notación científica[editar]

Adición y sustracción[editar]

Multiplicación[editar]

División[editar]

Exponenciación o Potenciación[editar]

Radicación[editar]

No hay comentarios:

Publicar un comentario